Summary

Liar’s Dice is a game based on luck but you can play smart. A good strategy is to start your bet with 25%~33% of the number of dice and call liar if the current bet is 40% of the number of dice or higher.

Introduction

When I was in high school, Liar’s Dice was a really popular game due to the Pirates of the Caribbean movies. As a nerd kid that had recently learned probability, I didn’t waste the opportunity to use math to play it better. In this post, I will show how I calculated optimal bets and a few strategies.

The game

You can check the game rules at its Wikipedia page, but the quick summary is that each player starts with 5 dice and the objective is to be the last player with dice remaining. Each round starts with all players rolling their dice while hiding the result from the other players. Then, the first player makes a bet about the number of dice that rolled a specific number. The next player can either call liar or make a higher bet. If a player calls liar, all the players reveal their dice and the bet is checked. If the bet is correct, the player that called liar loses a dice. Otherwise, the player that made the bet loses a dice. Importantly, the number 1 counts as a wild card.

The math

Assuming the dice are fair, the probability of a die rolling a chosen number \(d\) between 2 and 6 or a 1 is \(1/3\). So, in a round with \(n\) dice, the number of dice that rolled \(d\) or 1 is a random variable \(X\) that follows a binomial distribution

\[ X \sim \text{Binomial}(n, 1/3) \]

Then, for a given confidence level \(\alpha\) we can find the highest bet \(b\) such that the probability the bet being correct \(P(X \geq b)\) is equal to \(\alpha\) or higher. To do that, we can use the quantile function of the binomial distribution which is implemented in many programming languages like so

def calculate_optimal_bet(dice_count, confidence_level):
    optimal_bet = binomial(
        quantile=confidence_level,
        trial_count=dice_count,
        trial_success_probability=1/3,
        tail="right",
    )

    return optimal_bet

The strategy

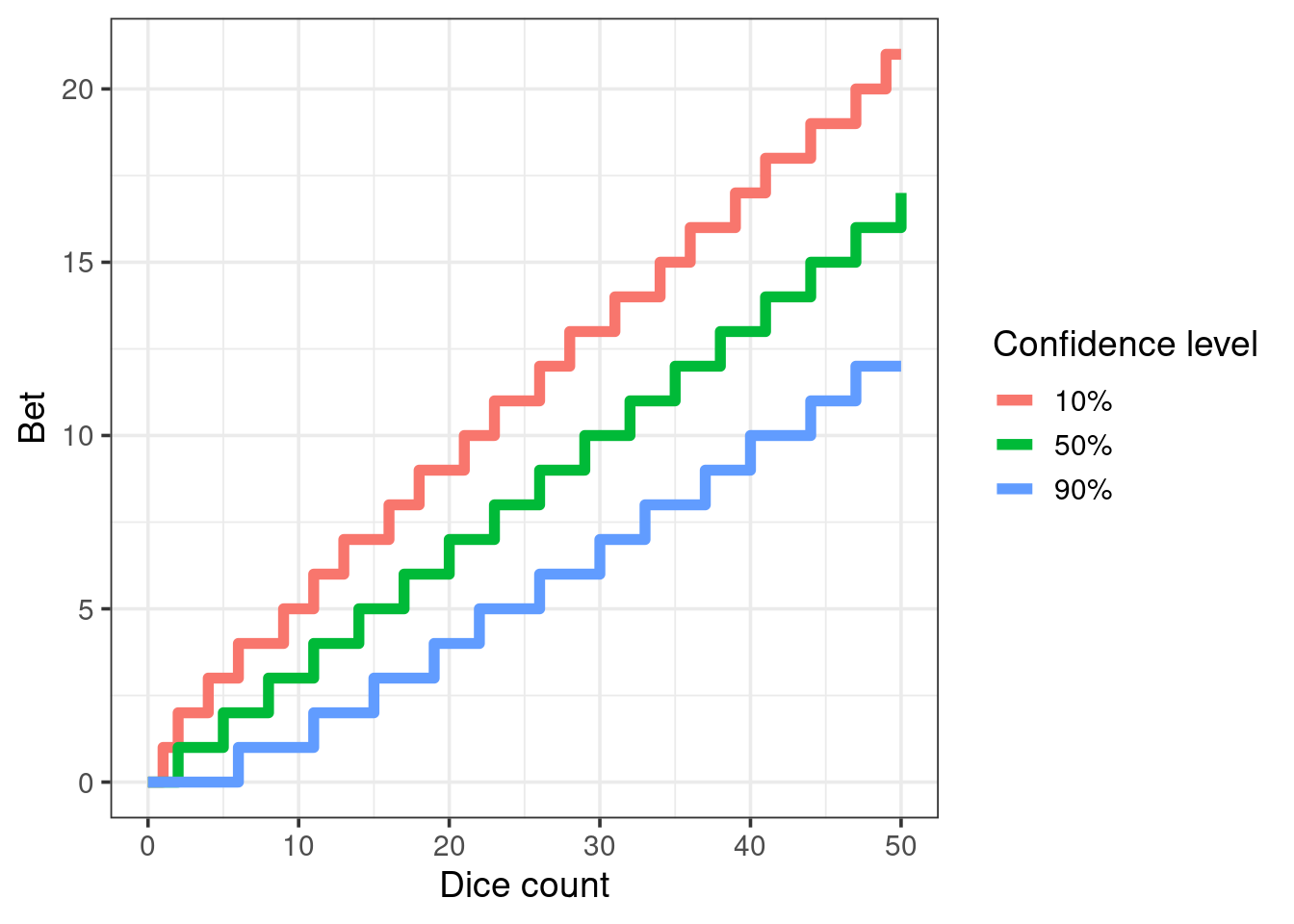
The following plot shows how the optimal bet changes with the number of dice and the confidence level. As expected, more dice allow for higher bets and the higher the confidence, the lower the bet should be.

A nice plot can give an intuition of how the optimal bet changes but it is not appropiate for an in game strategy. Instead, there are a few approximations that work surprisingly well (error <= 2):

10% of the time, there are 40% of the number of dice or more
50% of the time, there are 33% of the number of dice or more
90% of the time, there are 25% of the number of dice or more

So, a good strategy is to start your bet with 25% of the number of dice or even 33% of the number of dice to put maximum pressure on the next players. Moreover, you should call liar if the current bet is 40% of the number of dice or higher as it is very unlikely. Importantly, you can take into account the dice that you have to make a more accurate bet but keep in mind that you might reveal information about your hand in doing so.

Appendix

Approximation rules

We can regress the optimal bet on the dice count and the confidence level to find the approximation rules like so

optimal_bet ~ dice_count, for each confidence level

which yields the following coefficients

10% confidence level: 40.05%
50% confidence level: 33.38%
90% confidence level: 26.35%